wiki
cards are here
All thereoms, postulates, definitions, etc.
Postulates
$ Segment addition postulate
If B is between A and C, then AB + BC = AC
$ Angle addition postulate
If S in the interior of (\measuredangle PQS + \measuredangle SQR = \measuredangle PQR)
$ Two point postulate
Through any two points exists one line.
$ Line intersection postulate
If two lines intersect, then their intersection ie exactly one point
$ Three point postulate
Through any 3 non collinear points there exists exactly one plane
$ Plane point postulate
A plan contains at least three noncollinear points
$ Plane line postulate
If two points lie in a plane, then the line containing them lies in the plane.
$ Corresponding angles postulate
If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
Definitions
$ Definition of a linear pair
Two adjacent angles that add to 180
$ Definition of perpendicular lines
Two lines that intersect at right angles
$ Definition of supplementary angles
Two angles that add to 180
Theorems
$ Vertical angles congruence theorem (VACT)
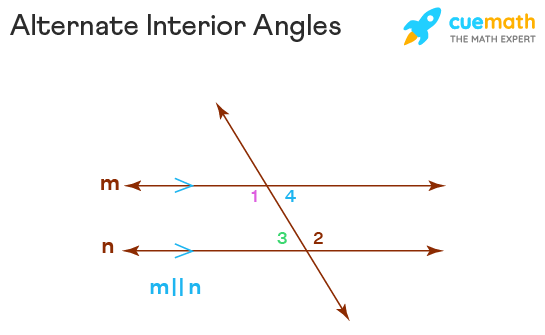
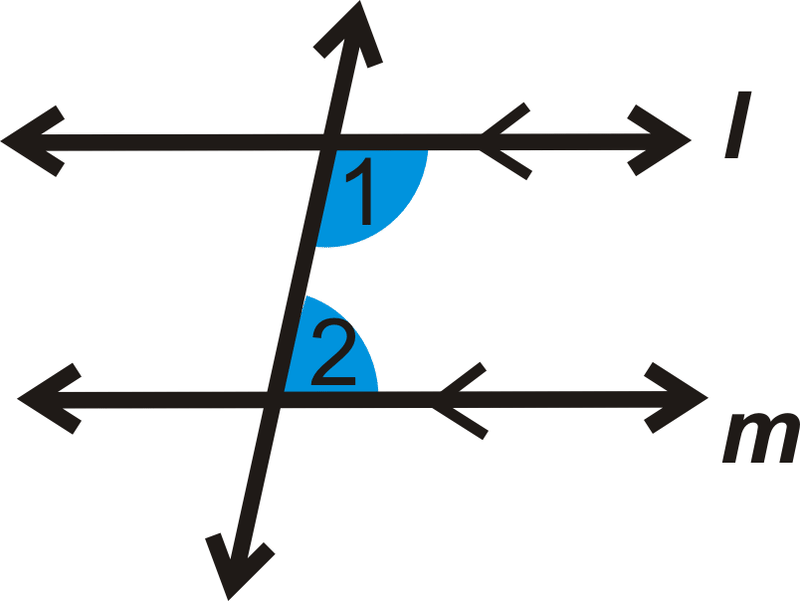
$ Alternate interior angles theorem
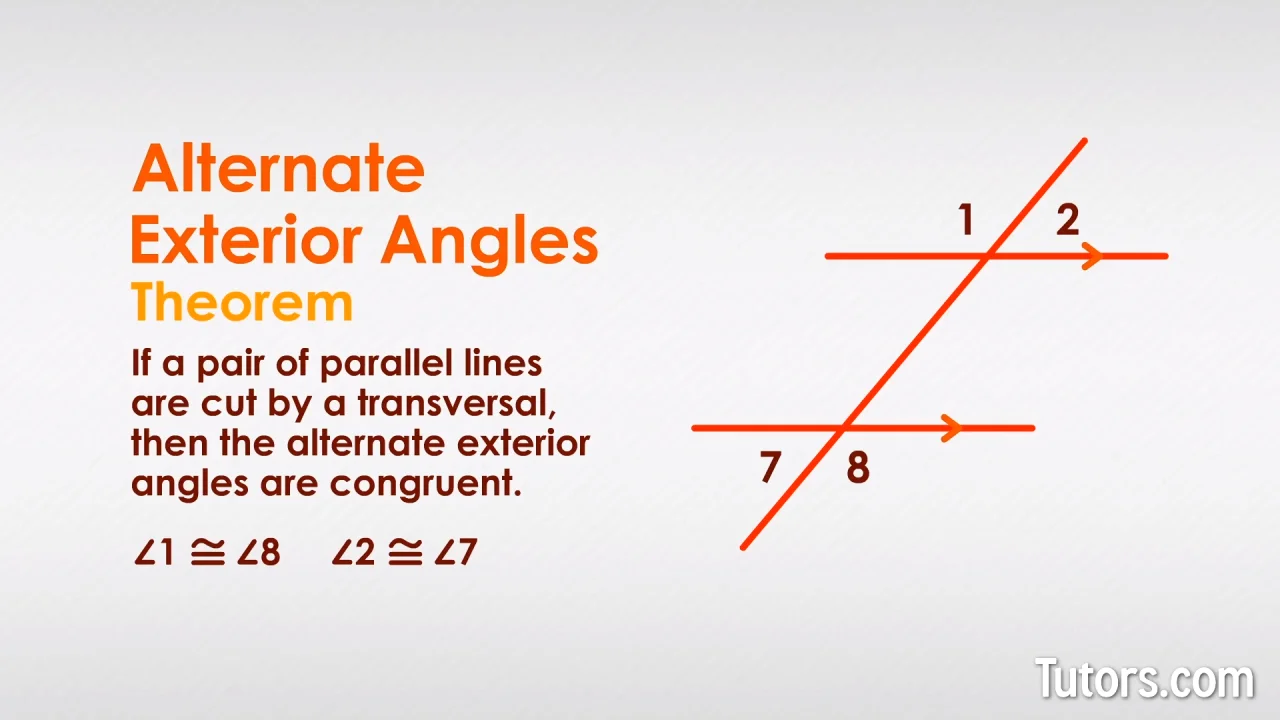
$ Alternate exterior angles theorem
$ Same side interior angles theorem
$ Triangle sum theorem
All interior angles of a triangle add to 180.
$ Exterior angles theorem
$ Side-Side-Side Congruence Theorem (SSS Congruence)
If the lengths of the sides of one triangle equal the lengths of the corresponding sides of another triangle, then the triangles are congruent.
$ Corresponding Parts of Congruent Triangles are Congruent (CPCTC)
corresponding parts of congruent triangles are congruent
$ Side-Angle-Side Congruence Theorem (SAS)
If two sides of one triangle and the angle between them are equal to the corresponding sides and agle of another triangle, then the two triangles are congruent.
$ Angle-Side-Angle Congruence Theorem (ASA)
If two angles of one triangle and the side between them are equal to the corresponding angles and side of another triangle, then the two triangles are congruent.
$ Angle-Angle-Side Congruence Theorem (AAS)
If two angles and a side of one triangle equal the corresponding angles and side in another triangle as shown below, then the triangles are congruent.